CLASIFICACIÒN DE CONJUNTOS

                             Clasificación de conjunto

Relaciones  de pertenecías

Para indicar que un objeto es un elemento de un conjunto se utiliza el símbolo ∈. Por ejemplo, para el conjunto A = {1,2,3,4,5,6}, podemos escribir 1 ϵ A, 2 ϵ A, …, 6 ϵ A.

Si un objeto no es un elemento del conjunto, lo indicaremos con el símbolo ∉. Así, para el conjunto anterior, escribiremos 0 ∉ A, - 3 ∉ A, ..

Determinación de conjuntos 

Hay dos formas de determinar conjuntos.

Por extensión ó Forma Tabular
Se dice que un conjunto es determinado por extensión (o enumeración), cuando se da una lista que comprende a todos los elementos del conjunto y sólo a ellos.

Ejemplos:
A = { a, e, i, o, u }
B = { 0, 2, 4, 6, 8 }

Por comprension ó Forma Constructiva
Se dice que un conjunto es determinado por comprensión, cuando se da una propiedad que la cumpla en todos los elementos del conjunto y sólo a ellos.

Ejemplos:
A = { x/x es una vocal }
B = { x/x es un número par menor que 10 } 

                        CLASE DE CONJUNTOS  

  

La clasificación de los conjuntos está fundamentada en el análisis de sus elementos o miembros,

                                                Conjunto Finito:
Cuando los miembros o elementos del conjunto se pueden contar o enumerar.
Por ejemplo el conjunto de las letras del alfabeto es un conjunto finito que expresado por comprensión es:
A = {x/x son las letras del alfabeto castellano}

                                                Conjunto Infinito:
 Cuando los elementos o miembros no se pueden enumerar o contar, se considera como conjunto infinito.
Un ejemplo de conjunto infinito son las estrellas del cielo. Los conjuntos infinitos siempre deberán determinarse por comprensión; para el ejemplo:
B = {x/x son las estrellas del universo}
                                               

                                               Conjunto Unitario:
 Es el conjunto que tiene un solo miembro o elemento. Un ejemplo:
C = {luna}
Conjunto Vacío:
Se trata del conjunto que no tiene elementos, o que estos son inexistentes, ejemplos:
D = {x/x son perros con alas}
E = { }
Se considera el conjunto vacío como subconjunto de cualquier conjunto.
                                               
                                                Conjunto Universal o Referencial: 

Se llama así al conjunto conformado por los miembros o elementos de todos los elementos que hacen parte de la caracterización.
Por ejemplo, dados:
A = {1, 3, 5, 7}        B = {2, 3, 4}        C = { 6, 7, 8, 9}
El conjunto universal o referencial es:
U ={1, 2, 3, 4, 5, 6, 7, 8, 9}

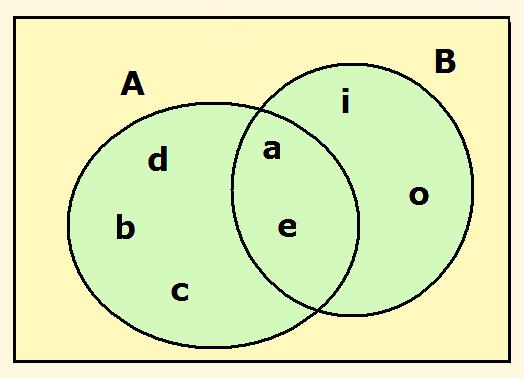
                    RELACIONES ENTRE CONJUNTOS

Al combinar y trabajar conjuntos, se establecen relaciones entre ellos. Estas relaciones se representan mediante símbolos para que al hacer operaciones, sepamos de qué se trata.

Por pertenecia 

Este símbolo se usa para representar que un elemento determinado hace parte del conjunto señalado.

Así mismo, representamos que un elemento no pertenece al conjunto señalado, escribiendo el mismo símbolo, pero con una línea cruzada en la mitad.

   POR Intersección 

Es el conjunto formado por los elementos comunes de A y B .

Unión 

Es el conjunto formado por los elementos que pertenecen tanto a A como a B