Reseña historica
En
la historia de las matemáticas se le dan créditos al matemático suizo
Leonhard Euler(1707-1783) por precisar el concepto de función, así como
por realizar un estudio sistemático de todas las funciones
elementales, incluyendo sus derivadas e integrales; sin embargo, el
concepto mismo de función nació con las primeras relaciones observadas
entre dos variables, hecho que seguramente surgió desde los inicios de
la matemática en la humanidad, con civilizaciones como la babilónica, la
egipcia y la china.
Par Ordenados
un
par ordenado es un conjunto de dos elementos A y B que tiene un orden,
al elemento A se lo llama primera componente y al elemento B segunda
componente. se lo representa simbólicamente .(a,b).
(a,b,c)
Producto Cartesiano de conjuntos
sea
2 conjuntos (A y B) no vacíos denominaremos producto cartesiano entre A
y B al conjunto de todos los pares ordenados cuya primera
componente pertenece al conjunto A y la segunda componente al conjunto B
, simbólicamente se lo representa .
AXB
ejemplo

ejemplo

Relaciones binarias
una relación establece la correspondencia entre los elementos de un conjunto no vació
A y B .
Generalmente al conjunto A se lo llama conjunto de partida y
al conjunto B conjunto de llegada simbólicamente se lo representa .
R ⊆ AXB

Definición matemática de Relación y de Función
En
matemática, Relación es la correspondencia de un primer conjunto,
llamado Dominio, con un segundo conjunto, llamado Recorrido o Rango,
de manera que a cada elemento del Dominio le corresponde uno o más
elementos del Recorrido o Rango.
Por su parte, una Función es una relación a la cual se añade la condición de que a cada valor del Dominio le corresponde uno y sólo un valor del Recorrido.
Por su parte, una Función es una relación a la cual se añade la condición de que a cada valor del Dominio le corresponde uno y sólo un valor del Recorrido.
Todas
las Relaciones pueden ser graficadas en el Plano Cartesiano.
Dados
dos conjuntos A y B una relación definida de A en B es un conjunto
de parejas ordenadas (par ordenado) que hacen verdadera una
proposición; dicho de otro modo, una relación es cualquier
subconjunto del producto cartesiano A x B
Ejemplo
1.
Si
A = {2, 3} y B = {1, 4, 5}, encontrar tres relaciones definidas
de A en B.
Solución
El
producto cartesiano de A x B está conformado por las siguientes
parejas o pares ordenados:
A
x B = {(2, 1), (2, 4), (2, 5), (3, 1), (3, 4), (3, 5)}
Y
cada uno de los siguientes conjuntos corresponde a relaciones
definidas de A en B:
R1 = {(2, 1), (3, 1)}
R2 = {(2, 4), (2, 5),
(3, 4), (3, 5)}
R3 = {(2, 4), (3, 5)}
- La relación R1 se puede definir como el conjunto de pares cuyo segundo elemento es 1, esto es, R1 = {(x, y) / y = 1}.
- La relación R2 está formada por los pares cuyo primer componente es menor que el segundo componente, R2 = {(x, y) / x < y}
- Y la relación R3 está conformada por todos los pares que cumplen con que el segundo componente es dos unidades mayor que el primer componente, dicho de otro modo, R3 = {(x, y) / y = x + 2}
DOMINIO Y RANGO DE UNA FUNCION
dominio de una relación es el conjunto de preimágenes;
es decir, el conjunto formado por los elementos del conjunto de
partida que están relacionados. Al conjunto de imágenes,
esto es, elementos del conjunto de llegada que están relacionados,
se le denomina recorrido o rango.
Ejemplo
3
Sea
A = {1, 2, 3, 4} y B = {4, 5, 6, 7, 8} y R la relación
definida de A en B determinada por la regla “y
es
el doble de x”
o “y
=
2x”,
encontrar dominio y rango de la relación.
Solución
El
total de pares ordenados que podemos formar, o producto cartesiano
es:
A
x B = {(1, 4), (1, 5), (1, 6), (1, 7), (1, 8), (2, 4), (2, 5),
(2, 6), (2, 7), (2, 8), (3, 4), (3, 5), (3, 6), (3, 7), (3, 8), (4,
4), (4, 5), (4, 6), (4, 7), (4, 8)}
Pero
los pares que pertenecen a la relación R (y = 2x) son solo:
R = {(2, 4), (3, 6), (4, 8)}
En
esta relación vemos que: “4 es el doble de 2”; esto es, “4 es
la imagen de 2 bajo R”, dicho de otro modo, “2 es preimagen de
4”.
Así,
el dominio y rango son:
D = {2, 3, 4}
Rg
= {4, 6, 8}
Según
lo que vemos, ¿Qué relación hay entre el Dominio y el conjunto de
partida?
En
el Dominio falta el elemento 1 del conjunto de partida, por lo tanto
el Dominio es un subconjunto de A.
Otra
pregunta: ¿Todo elemento del conjunto de llegada es elemento del
rango?
La
respuesta es no, pues en el rango faltan el 5 y el 7.
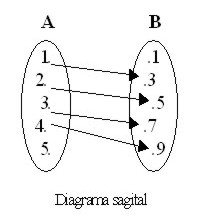
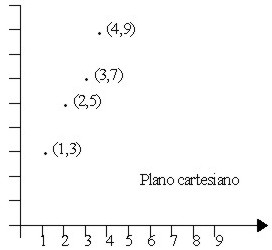
Representación gráfica de las relaciones
Los
pares ordenados se pueden representar gráficamente por medio de
diagramas sagitales o por medio de puntos en el plano cartesiano.
Veamos el siguiente ejemplo.
Ejemplo
4
Si
A = {1, 2, 3, 4, 5} y B = {1, 3, 5, 7, 9} y R la relación
definida por la regla
R
= {(x,
y)
/ y
=
2x
+
1}, graficar R.
Solución
Los
pares ordenados que pertenecen a la relación (que cumplen con
y = 2x + 1) son:
R
= {(1, 3), (2, 5), (3, 7), (4, 9)}
Y
la gráfica correspondiente es la siguiente:
Dominio y rango
 |
Lo que puede entrar en una función se llama el dominio |
 |
Lo que es posible que salga de una función se llama el codominio |
 |
Lo que en realidad sale de una función se llama rango o imagen |
Parte de la función
De hecho el dominio es una parte esencial de la función. Un dominio diferente da una función diferente.
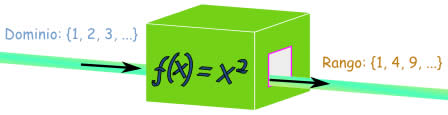
Ejemplo: una simple función como f(x) = x2 puede tener dominio (lo que entra) los números de contar {1,2,3,...}, y el rango será entonces el conjunto {1,4,9,...}

Codominio y rango
El codominio es el conjunto de valores que podrían salir.
El rango es el conjunto de valores que realmente salen.
Ejemplo: puedes definir una función f(x)=2x con dominio y codominio los enteros (porque tú lo eliges así).
Pero si lo piensas, verás que el rango (los valores que salen de verdad) son sólo los enteros pares.
Así que el codominio son los enteros (lo has elegido tú) pero el rango son los enteros pares.
La importancia del codominio
Si tú dices que el codominio (las salidas posibles) es el conjunto de los números reales, ¡entonces la raíz cuadrada no es una función! ... ¿te sorprende?
La razón es que podría haber dos respuestas para una entrada, por ejemplo f(9) = 3 o -3
√De hecho, el símbolo radical (como en √x) siempre significa la raíz cuadrada positiva (la principal), así que √x es una función porque su codominio es correcto.
Así que el codominio que elijas puede afectar el que algo sea o no una función.
Notación
A los matemáticos no les gusta escribir muchas palabras cuando unos pocos símbolos hacen el mismo trabajo. Así que hay maneras de decir que "el dominio es", "el codominio es", etc.Esta es la mejor manera que conozco:
| Esto dice que la función "f" tiene dominio "N" (los números naturales), y también codominio "N". | |
| y esto dice que la función "f" toma "x" y devuelve "x2" |
TIPOS DE FUNCIONES
Inyectivo, sobreyectivo y biyectivo
"Inyectivo, sobreyectivo y biyectivo" te dan información sobre el comportamiento de una función.
Puedes entender una función como una manera de conectar elementos de un conjunto "A" a los de otro conjunto "B":
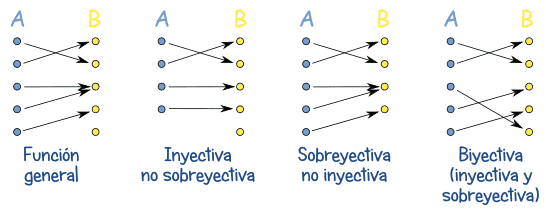
"Sobreyectivo" significa que cada elemento de "B" tiene por lo menos uno de "A" (a lo mejor más de uno). "Biyectivo" significa inyectivo y sobreyectivo a la vez. Así que hay una correspondencia perfecta "uno a uno" entre los elementos de los dos conjuntos.
Definiciones formales
Inyectivo
Ejemplo: f(x) = x2 del conjunto de los números naturales  a
a  es una función inyectiva.
es una función inyectiva.
(Pero f(x) = x2 no es inyectiva cuando es desde el conjunto de enteros 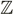 (esto incluye números negativos) porque tienes por ejemplo
(esto incluye números negativos) porque tienes por ejemplo
- f(2) = 4 y
- f(-2) = 4)
Nota: inyectiva también se llama "uno a uno", pero esto se confunde porque suena un poco como si fuera biyectiva.
Sobreyectivo (o también "epiyectivo")
Ejemplo: la función f(x) = 2x del conjunto de los números naturales  al de los números pares no negativos es sobreyectiva.
al de los números pares no negativos es sobreyectiva.
Sin embargo, f(x) = 2x del conjunto de los números naturales a
a  no es sobreyectiva, porque, por ejemplo, ningún elemento de
no es sobreyectiva, porque, por ejemplo, ningún elemento de  va al 3 por esta función.
va al 3 por esta función.
Sin embargo, f(x) = 2x del conjunto de los números naturales
Biyectiva
(Pero no desde el conjunto de todos los números reales porque podrías tener por ejemplo
- f(2)=4 y
- f(-2)=4)
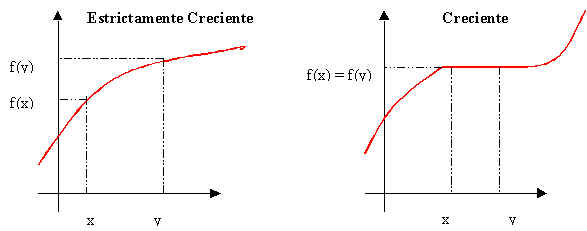
FUNCIÓN CRECIENTE
- Una función y=f(x) es creciente cuando al aumentar la variable independiente, x, aumenta la variable dependiente, y.
- Una función y=f(x) es decreciente cuando al aumentar la variable independiente, x, disminuye la variable dependiente, y.
- Una función y=f(x) es constante cuando al aumentar la variable independiente, x, la variable dependiente, y, no varía.
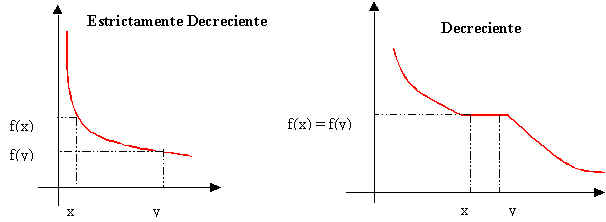
FUNCIÓN MONÓTONA
Se dice que F
es una función monótona en un intervalo I , si y solo si F es
estrictamente creciente o estrictamente decreciente en ese intervalo.
- Par e Impar
Se dice que una función es par si f(x) = f(-x), en el caso de que f(x) = -f(-x) se dice que la función es impar.
Ejemplos 1:
La función y(x)=x es impar ya que:
f(-x) = -x
pero como f(x) = x entonces:
f(-x) = - f(x).

Ejemplo 2:
Otra función impar es y = 1/x
Cuando f(x) = -f(-x)

Ejemplo 3:
La función f(x)=x2 es par ya que f(-x) = (-x)2 =x2

- Función periódica

La función se repite de T en T, siendo T el período.
Ejemplos
1. La función f(x) = x − E(x), es periódica de periodo 1.

2. sen (x + 2π) = sen x

En el caso de la función seno T = 2π
- Funciones por Tramos
Son funciones definidas por distintos criterios, según los intervalos que se consideren.
 El dominio lo forman todos los números reales menos el 2.
El dominio lo forman todos los números reales menos el 2.
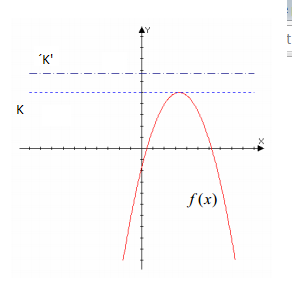
- FUNCIÓN ACOTADA SUPERIORMENTE
Definición: Decimos que una función está acotada superiormente si existe un valor K tal que no es superado por ningún valor de la función, es decir: f(x)≤K para todo valor de x perteneciente al dominio, como podemos ver en la siguiente imagen:
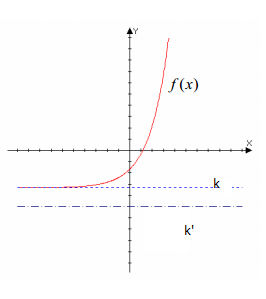
FUNCIÓN ACOTADA INFERIORMENTE
Definición: Decimos que una función está acotada inferiormente si existe un valor k tal que no hay ningún valor de la función que sea inferior a k, es decir: f(x)≥k para todo valor de x perteneciente al dominio, como podemos ver en la siguiente imagen:
función lineales
Sea A y B numero reales la función f: R —> R / f(x) = a.x+b donde a y b son números reales, es una función lineal.

ejemplos:
f (x) = 5x + 13
m = la pendiente es 5
b = 13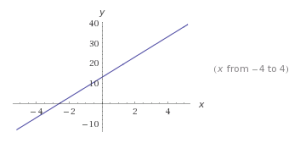


para los cortes Y se utiliza  ejemplos
ejemplos
 ejemplos
ejemplos
(A>o)^(b>0)

b) ; (a>o)^(b>0)
C):(a<0)^(b>0)