Reseña
histórica de los números reales
Los números reales son aquellos que poseen una expresión decimal. En
matemáticas los números reales influyen tanto números racionales como a los
números irracionales, aquellos que no se pueden expresar e manera fraccionaria
tiene infinitas cifras decimales.
Durante los siglos XVI y XVII el cálculo avanzo mucho aunque carecía de una
base rigurosa, ya que en el momento no se consideraba necesario el formalismo
de la actualidad, usando como expresiones como pequeño, límite, etc. Si una
definición precisa, esto llevo unas series de problemas lógica que hicieron
evidente la necesidad crear una base rigurosa de la nueva matemática.
Los números relés como un campo
axioma de los numeroe reales
En matemáticas, un axioma es una premisa que, por considerarse evidente, se
acepta sin demostración, como punto de partida para demostrar otras fórmulas.
Tradicionalmente, los axiomas se eligen de entre las consideradas “verdades
evidentes” porque permiten deducir las demás formulas.
En lógica matemática, un postulado es un proposición, no necesariamente
evidente: una fórmula bien formada de un lenguaje formal utilizada en una
deducción para llegar a una conclusión.
En el campo de los números reales son seis los principales axiomas que se
toman, y a través de su uso y postulación, permiten el desarrollo de los
teoremas que estructuran una parte de las matemáticas.
Los seis axiomas son:
Axioma 1. Si a, b
ϵ , entonces a + b, ab ϵ
(Ley de cerradura para la suma y el producto)
Demostración/:
TEOREMA 3
En los números reales distintos de cero se cumplen las leyes cancelativas y uniforme con la multiplicación, es decir:
i)Six•y=x•zentoncesy=z.
ii) Si y=z entonces x•y=x•z.
Axioma 2. Si a, b
ϵ entonces a+b = b+a y ab = ba
(Ley de conmutatividad)
Axioma 3. Si a, b, c ϵR entonces a(b+c) =
(a+b)+c y a(bc) = (ab)c
(Ley de asociatividad)
Axioma 4. Si a, b, c
ϵ entonces a(b + c) = ab + ac
(Ley de distributividad)
Axioma 5. Existen 0, 1
ϵ , con 0 ̸= 1, tales que: si a ϵR, entonces a+0
= a y a·1 = a
(0 se llamará Neutro aditivo y 1 se
llamará Neutro multiplicativo)
Axioma 6. Si a ϵ ,
existe a1 ϵ tal que a + a1 = 0 y si a
ϵ con a ̸= 0, entonces existe a2 ϵ
tal que a · a2 = 1
(Existencia de los inversos)
TEOREMAS DE NUMEROS REALES
TEOREMA 1
En los
números reales se cumplen las leyes cancelativas y uniforme con la suma, es
decir:
i) Si x+y=x+z entonces y=z.
ii) Si y=z entonces x+y=x+z.
Demostración/:
i)
y=0+y
y=((-x)+x)+y
y=(-x)+(x+y)
y=(-x)+(x+z)
y=(-x)+(x+z)
y=((-x)+x)+z
y==0+z
y==z
y=0+y
y=((-x)+x)+y
y=(-x)+(x+y)
y=(-x)+(x+z)
y=(-x)+(x+z)
y=((-x)+x)+z
y==0+z
y==z
La anterior
demostración se justifica usando el axioma 4, el axioma 5, ley asociativa, la
hipótesis, ley asociativa, el axioma 5 y el axioma 4 respectivamente.
ii) Por ley reflexiva x+z=x+z
pero como z=y entonces por ley transitiva x+z= x+y.
TEOREME 2
Los neutros e inversos aditivos y multiplicativos son únicos.
Los neutros e inversos aditivos y multiplicativos son únicos.
Demostración/:
Supongamos
que existen 01 y 02 dos neutros aditivos, entonces 01 + 02 = 01 y 02
+01 = 02 luego por ley transitiva y conmutativa 01= 01 + 02=02 +01 = 02.luego
estos neutros aditivos son el mismo. (Análogamente se demuestra para el neutro
multiplicativo).
Ahora supongamos que para x hay dos inversos aditivos x1 y x2 tal que x+ x1 = 0 y x+ x2 = 0 por ley transitiva tenemos que x+ x1 = x+ x2 luego por ley cancelativa x1 = x2. Luego los inversos aditivos para x real son el mismo. (Análogamente se demuestra para el inverso multiplicativo teniendo en cuenta que x≠0)
Ahora supongamos que para x hay dos inversos aditivos x1 y x2 tal que x+ x1 = 0 y x+ x2 = 0 por ley transitiva tenemos que x+ x1 = x+ x2 luego por ley cancelativa x1 = x2. Luego los inversos aditivos para x real son el mismo. (Análogamente se demuestra para el inverso multiplicativo teniendo en cuenta que x≠0)
TEOREMA 3
En los números reales distintos de cero se cumplen las leyes cancelativas y uniforme con la multiplicación, es decir:
i)Six•y=x•zentoncesy=z.
ii) Si y=z entonces x•y=x•z.
Demostración/:
La denostación es análoga a la del Teorema1
La denostación es análoga a la del Teorema1
TEOREMA 4
-0=0.
TEOREMA 6
Para x, y reales se cumple: (-x) •y= x• (-y) = -(x•y).
TEOREMA 7
Para x≠0 real se cumple: 1/(1/x)= x.
1/(x•y)=(x•(1/x))•(y•(1/y))•1/(x•y)
1/(x•y)=(x•y)•((1/x)•(1/y))•1/(x•y)
1/(x•y)=((1/x)•(1/y))•((x•y)•1/(x•y))
1/(x•y)=(1/x)•(1/y).
Aquí hemos usando en repetidas ocasiones propiedades como la ley conmutativa y asociativa para el producto y la existencia de los neutros e inversos multiplicativos.
TEOREMA 10
Para x, z reales y w, y reales distintos de cero se cumple
TEOREMA 11
Para x, z real y w, y reales distintos de cero se cumple:
TEOREMA 12
Para x, y y z reales se cumple: x>y si y solo si x+z>y+z.
i) Si x•y>0 con x>0 entonces y>0.
ii) Si x•y>0 con 0>x entonces 0>y.
iii) Si 0> x•y con x>0 entonces 0>y.
iv) Si 0> x•y con 0>x entonces y>0.
Demostración/:
Supongamos que no se cumple la tesis, es decir, 0>y como x>0 entonces por teorema 13 0>x•y llegando a la contradicción de la hipótesis o sea que lo afirmamos anteriormente es falso, llegando a la demostración del teorema (análogamente se demuestra para ii), iii) y iv).
TEOREMA 15
Para x≠0 real se cumple: x²>0.
Demostración/:
Tenemos que 0+ (-0) = 0 y 0+0 = 0 luego por ley transitiva 0+ (-0) = 0+0, finalmente por ley cancelativa 0 = -0.
TEOREMA 5
Para x real se cumple: -(-x)= x.
Tenemos que 0+ (-0) = 0 y 0+0 = 0 luego por ley transitiva 0+ (-0) = 0+0, finalmente por ley cancelativa 0 = -0.
TEOREMA 5
Para x real se cumple: -(-x)= x.
Demostración/:
– (-x) = 0+
(– (-x))=(x+ (-x))+ (– (-x))= x+ ((-x)+ (– (-x)))= x+0=podemos ver que usamos los axiomas 4 y
5 y el hecho de que (– (-x)) es el inverso aditivo de (-x).
LEMA
Para toda x
real se cumple: x•0=0•x=0.
Demostración/:
x•0=x• (0+0) = x•0+x•0, luego x•0 = x•0+x•0 y por ley cancelativa 0 = x•0 ò x•0=0, de la misma forma demostramos que 0•x=0, por lo que concluimos que x•0=0•x=0.
Demostración/:
x•0=x• (0+0) = x•0+x•0, luego x•0 = x•0+x•0 y por ley cancelativa 0 = x•0 ò x•0=0, de la misma forma demostramos que 0•x=0, por lo que concluimos que x•0=0•x=0.
TEOREMA 6
Para x, y reales se cumple: (-x) •y= x• (-y) = -(x•y).
Demostración/:
Por lema 0=0•y=(x+(-x)) 0•y = x•y+(-x) •y, entonces 0= x•y+(-x)•y y por ley uniforme se puede sumar -(x•y) y tenemos que -(x•y) = (-(x•y))+x•y+(-x)•y luego (x•y))+x•y=0 por lo que se tiene que: -(x•y) = 0+(-x)•y =+(-x)•y. Análogamente se demuestra que x•(-y)= -(x•y).
Por lema 0=0•y=(x+(-x)) 0•y = x•y+(-x) •y, entonces 0= x•y+(-x)•y y por ley uniforme se puede sumar -(x•y) y tenemos que -(x•y) = (-(x•y))+x•y+(-x)•y luego (x•y))+x•y=0 por lo que se tiene que: -(x•y) = 0+(-x)•y =+(-x)•y. Análogamente se demuestra que x•(-y)= -(x•y).
TEOREMA 7
Para x≠0 real se cumple: 1/(1/x)= x.
Demostración/:
Esta
demostración es parecida al teorema 5.
TEOREMA 8
Para x, y reales distintos de cero se cumple: 1/(x•y)= (1/x) • (1/y).
TEOREMA 8
Para x, y reales distintos de cero se cumple: 1/(x•y)= (1/x) • (1/y).
Demostración/:
1/(x•y)=1•1•1/(x•y)1/(x•y)=(x•(1/x))•(y•(1/y))•1/(x•y)
1/(x•y)=(x•y)•((1/x)•(1/y))•1/(x•y)
1/(x•y)=((1/x)•(1/y))•((x•y)•1/(x•y))
1/(x•y)=(1/x)•(1/y).
Aquí hemos usando en repetidas ocasiones propiedades como la ley conmutativa y asociativa para el producto y la existencia de los neutros e inversos multiplicativos.
TEOREMA 9
Para x, y reales distintos de cero se cumple: 1/(x/y)= y/x.
Para x, y reales distintos de cero se cumple: 1/(x/y)= y/x.
Demostración/:
Aquí vemos como los Teoremas 7 y 8 son usados junto con las propiedades conmutativa y asociativa del producto para demostrar lo requerido.
Aquí vemos como los Teoremas 7 y 8 son usados junto con las propiedades conmutativa y asociativa del producto para demostrar lo requerido.
1/(x/y)=
1/(x • (1/y))= (1/x) • (1/(1/y))= (1/x) •y = y/x.
TEOREMA 10
Para x, z reales y w, y reales distintos de cero se cumple
: X/y +
z/w = (x•w+ z•y)/ y•w.
Demostración/:
(x/y)+(z/w)=(x/y+z/w)•1
(x/y)+(z/w)=(x/y+z/w)•((y•w)(1/y•w))
(x/y)+(z/w)=((x/y+z/w)(y•w))(1/y•w)
(x/y)+(z/w)=(x/y•(y•w)+z/w•(y•w))(1/y•w)
(x/y)+(z/w)=(x•w+y•z)(1/y•w)
(x/y)+(z/w)=(x•w+y•z)/(y•w)
Note que en esta demostración usamos los axiomas 2, 3, 6 y 7.
(x/y)+(z/w)=(x/y+z/w)•1
(x/y)+(z/w)=(x/y+z/w)•((y•w)(1/y•w))
(x/y)+(z/w)=((x/y+z/w)(y•w))(1/y•w)
(x/y)+(z/w)=(x/y•(y•w)+z/w•(y•w))(1/y•w)
(x/y)+(z/w)=(x•w+y•z)(1/y•w)
(x/y)+(z/w)=(x•w+y•z)/(y•w)
Note que en esta demostración usamos los axiomas 2, 3, 6 y 7.
TEOREMA 11
Para x, z real y w, y reales distintos de cero se cumple:
(X/y)•
(z/w)= (x•z)/ (y•w).
Demostración/:
Al igual que
en el teorema anterior aquí usamos la definición 5 los axiomas 2, 3 y los
teoremas 8 y 9.
(x/y)•(z/w)=((x/y)•z)/w
(x/y)•(z/w)= ((x•(1/y))•z)/w
(x/y)•(z/w)= (x•((1/y)•z)/w
(x/y)•(z/w)= (x•(z/y))/w
(x/y)•(z/w)= ((x•z)/y)/w
(x/y)•(z/w)= x•z/y•w.
(x/y)•(z/w)=((x/y)•z)/w
(x/y)•(z/w)= ((x•(1/y))•z)/w
(x/y)•(z/w)= (x•((1/y)•z)/w
(x/y)•(z/w)= (x•(z/y))/w
(x/y)•(z/w)= ((x•z)/y)/w
(x/y)•(z/w)= x•z/y•w.
TEOREMA 12
Para x, y y z reales se cumple: x>y si y solo si x+z>y+z.
Demostración/:
Sea a= x+z y b= y+z, entonces a-b=(x+z)-(y+z)=x-y como a>b si y solo si a-b>0 y por transitividad de a>b se deduce que x+z>y+z.
Por otro lado veamos que x+z > y+z si y solo si (x+z)-(y+z) >0 luego x-y >0 x>y.
Sea a= x+z y b= y+z, entonces a-b=(x+z)-(y+z)=x-y como a>b si y solo si a-b>0 y por transitividad de a>b se deduce que x+z>y+z.
Por otro lado veamos que x+z > y+z si y solo si (x+z)-(y+z) >0 luego x-y >0 x>y.
ii) 0>x si y solo si 0> (1/x). TEOREMA
13
Para x, y
y z reales con z distinto de cero se cumple:
i) x>y si y solo si x•z>y•z
con z>0.
ii) x>y si y solo si y•z
> x•z con 0>z.
Demostración/:
Demostración/:
Si x>y
si y solo si x-y >0 por lo tanto x-y es positivo, si z>0
entonces z también es positivo y por los axiomas de orden vemos que (x-y)•z
es positivo si y solo si (x-y)•z >0
Si y solo si x •z -y•z>0 si y solo si x •z >y•z.
Si x>y si y solo si x-y >0 por lo tanto x-y es positivo, 0>z entonces (-z)>0 usando el mismo razonamiento que en i) llegamos a que y•z-x•z>0 si y solo si y•z >x•z.ii) se deduce de la misma forma.
Si y solo si x •z -y•z>0 si y solo si x •z >y•z.
Si x>y si y solo si x-y >0 por lo tanto x-y es positivo, 0>z entonces (-z)>0 usando el mismo razonamiento que en i) llegamos a que y•z-x•z>0 si y solo si y•z >x•z.ii) se deduce de la misma forma.
TEOREMA 14
Para x, y reales distintos de cero se cumple:
Para x, y reales distintos de cero se cumple:
i) Si x•y>0 con x>0 entonces y>0.
ii) Si x•y>0 con 0>x entonces 0>y.
iii) Si 0> x•y con x>0 entonces 0>y.
iv) Si 0> x•y con 0>x entonces y>0.
Demostración/:
Supongamos que no se cumple la tesis, es decir, 0>y como x>0 entonces por teorema 13 0>x•y llegando a la contradicción de la hipótesis o sea que lo afirmamos anteriormente es falso, llegando a la demostración del teorema (análogamente se demuestra para ii), iii) y iv).
TEOREMA 15
Para x≠0 real se cumple: x²>0.
Demostración/:
Si x>0
entonces x es positivo luego y·w=x² es positivo si y solo si x²>0.Si
0>x entonces (-x) es positivo luego (-x)•(-x)=(-x)² es
positivo si y solo si (-x)²>0.Pero (-x)•(-x)=-(x•(-x))=-(-(x•x))=x•x=x²
por teorema 6, con lo que vemos que (-x)•(-x)= x²>0.
TEOREMA 16
Para x≠0 real se cumple:
i) x>0 si y solo si (1/x)>0.
a = c → a - b = c - d
a = c → a + b = c + d
TEOREMA 16
Para x≠0 real se cumple:
i) x>0 si y solo si (1/x)>0.
Razones y proposiciones
Definición de
razón
Una razón matemática
es el cociente entre dos medidas de diferentes magnitudes. Generalmente, se
expresa como «a es a b».
En una razón al
primer término se le llama antecedente y al segundo se llama consecuente.
a
Antecedente
b
Consecuente
DEFINICION DE PROPORSICION
De proposición La proporción muestra los
tamaños relativos de dos o más valores.
Las proporciones pueden mostrarse de diferentes maneras. Usando el ":" para separar los valores, o como un solo número dividiendo un valor para el total.
Ejemplo: si hay un niño y tres niñas la proporción podría escribirse así:
1:3 (por cada niño hay 3 niñas)
1/4 son niños y 3/4 son niñas
0.25 son niños (dividiendo 1 por 4)
25% son niños (0.25 como porcentaje)
Las proporciones pueden mostrarse de diferentes maneras. Usando el ":" para separar los valores, o como un solo número dividiendo un valor para el total.
Ejemplo: si hay un niño y tres niñas la proporción podría escribirse así:
1:3 (por cada niño hay 3 niñas)
1/4 son niños y 3/4 son niñas
0.25 son niños (dividiendo 1 por 4)
25% son niños (0.25 como porcentaje)
PROPIEDADES
DE LA PROPOSICIONES
Propiedad 1: en toda proporción
, la suma o diferencia entre el antecedente y el consecuente de la primera
razón es a su consecuente, como la suma o diferencia entre el antecedente y el
consecuente de la segunda razón es a su consecuente.
a = c
→ a + b = c + d
b
d
b d
a = c → a - b = c - d
b
d
b d
Propiedad 2 : en toda proporción , la suma o diferencia
entre el antecedente y el consecuente de la primera razón es a su antecedente ,
como la suma o diferencia entre el antecedente y el consecuente de la segunda
razón es a su antecedente .
a = c → a + b = c + d
b
d
a c
a = c → a
- b = c - d
b
d
a c
Propiedad 3 : en toda proporción, la suma entre
el antecedente y el consecuente de la primera razón es a la diferencia entre
los mismos , como la suma entre el antecedente y el consecuente de la segunda
razón es a la diferencia de los mismos .
a = c → a
+ b = c + d
b
d a - b
c - d
intervalos
Los intervalos están determinados por dos números que se
llaman extremos. En un intervalo se encuentran todos los números comprendidos
entre ambos y también pueden estar los extremos.
Intervalo abierto
Intervalo abierto, (a, b), es el conjunto de todos los números reales
mayores que a y menores que b.
(a, b) = {x 
 / a < x < b}
/ a < x < b}
Intervalo cerrado
Intervalo cerrado, [a, b], es el conjunto de todos los números reales
mayores o iguales que a y menores o iguales que b.
[a, b] = {x 
 / a ≤ x ≤ b}
/ a ≤ x ≤ b}
Intervalo semiabierto por la izquierda
Intervalo semiabierto por la izquierda, (a, b], es el conjunto de todos
los números reales mayores que a y menores o iguales que b.
(a, b] = {x 
 / a < x ≤ b}
/ a < x ≤ b}
Intervalo semiabierto por la derecha
Intervalo semiabierto por la derecha, [a, b), es el conjunto de todos los
números reales mayores o iguales que a y menores que b.
[a, b) = {x 
 / a ≤ x < b}
/ a ≤ x < b}
queremos nombrar un conjunto de puntos formado por dos o
más de estos intervalos, se utiliza el signo  (unión Cuando)
entre ellos.
(unión Cuando)
entre ellos.
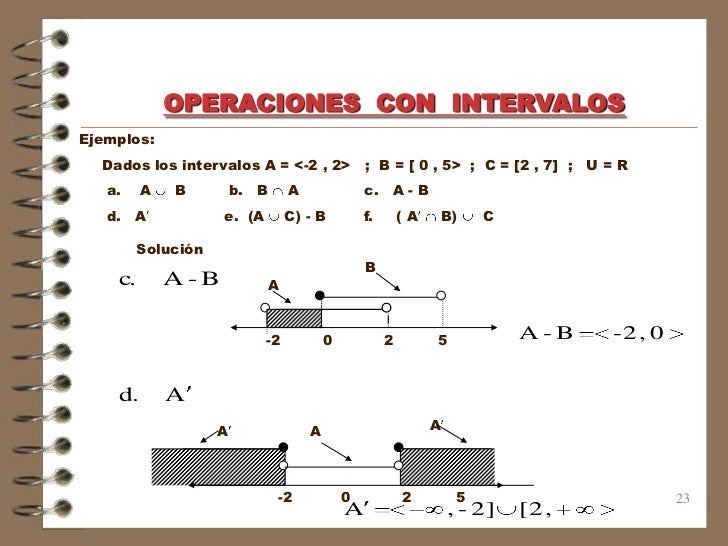
operaciones com intervalos
También se puede entender al valor absoluto como la distancia que existe entre el número y 0. El número 563 y el número -563 están, en una recta numérica, a la misma distancia del 0. Ese, por lo tanto, es el valor absoluto de ambos: |563|.
La distancia que existe entre dos numeros reales, por otra parte, es el valor absoluto de su diferencia. Entre 8 y 5, por ejemplo, hay una distancia de 3. Esta diferencia tiene un valor absoluto de |3|.
Usando la definición de valor absoluto se tiene:
Ecuaciones con valor absoluto de la forma │ax + b│= c
Ecuaciones
Según los
expertos en Matemática, una ecuación (concepto derivado del latín
aequatio) constituye una igualdad donde aparece como mínimo una
incógnita que exige ser develada por quien resuelve el ejercicio. Se conoce
como miembros a cada una de las expresiones algébricas que permiten
conocer los datos (es decir, los valores ya conocidos) y las incógnitas (los
valores que no se han descubierto) vinculados a través de diversas operaciones
matemáticas.
Cabe
resaltar que los datos incluidos en una ecuación pueden ser números,
constantes, coeficientes o variables. Las incógnitas, por su parte,
están representadas por letras que sustituyen al valor que se intenta hallar.
Una ecuación
sencilla es la siguiente:
4 + x = 9
En dicha
ecuación, 4 y 9 son los datos, mientras que x es la
incógnita. La ecuación puede resolverse de la siguiente forma:
4 + x = 9
x = 9 – 4
x = 5
El valor
de la incógnita, por lo tanto, es 5.
Tipos de ecuaciones
Ecuaciones
algebraicas: este tipo
de ecuaciones, como su nombre lo indica, son todas aquellas que se basan en
operaciones algebraicas y que tienen un cuerpo del tipo P=0. Este tipo de
ecuaciones son las más comunes.
Ecuaciones
polinómicas: este tipo
de ecuaciones son en realidad parte de las algebraicas. Se caracterizan porque
el polinomio, como su nombre lo indica, es un elemento que tiene diversas variables.
Es decir, son las ecuaciones que tienen coeficientes racionales o cuya
operación se hace así.
Ecuaciones
de primer grado: las
ecuaciones de este tipo se definen como aquellas que presentan un planteamiento
de igualdad donde existe una o más variables a la primera potencia. Por lo
tanto, las ecuaciones de este tipo se resuelven únicamente con sumas y restas
de variables que están expresadas a la primera potencia. También son conocidas
como ecuaciones lineales.
Ecuaciones
de segundo grado: como su
nombre lo indica, este tipo de ecuaciones son aquellas que tienen la forma de
una suma algebraica cuyo grado máximo es dos. Esto quiere decir que están
representadas por un polinomio de segundo grado o cuadrático. Es por ello que a
este tipo de ecuaciones también se les conoce como cuadráticas.
Ecuaciones
diofánticas: son las
ecuaciones que tienen generalmente distintas variables que se plantean según
número enteros o naturales. De esta manera, las ecuaciones diofánticas tienen
una solución expresada en números enteros.
Ecuaciones
racionales: este tipo
de ecuaciones son aquellas que tienen una o más incógnitas que no son
únicamente algebraicas sino que pueden ser de otro tipo, aunque su solución
únicamente se puede hacer mediante el álgebra.
Ecuaciones
diferenciales: son el tipo
de ecuación que cuyas derivadas que tienen una o más funciones desconocidas. A
su vez, este tipo de ecuaciones se subdividen en ordinarias y parciales.
Ecuaciones
integrales: como su
nombre lo establece, este tipo de ecuaciones se caracterizan porque su
incógnita aparece dentro de una integral.
Ecuaciones
funcionales: este tipo
de ecuaciones son muy similares a las integrales. En ellas se de una
combinación de variables independientes y funciones incógnitas. En este caso se
trata de ecuaciones que muchas veces no pueden ser reducidas a resoluciones
algebraicas como tal.
Proceso para resolver una ecuacion
El conjunto solución es aquel que contiene todos los valores determinados que cumplen con la ecuación, y estos valores son denominados soluciones. Por ejemplo, la ecuación
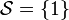 como su conjunto solución, con 1 como única solución de la ecuación.
como su conjunto solución, con 1 como única solución de la ecuación.
En general, dada una función, y
una función, y 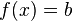 la ecuación que determina.
la ecuación que determina.
El conjunto de valores de A es el conjunto solución si se cumple
de valores de A es el conjunto solución si se cumple 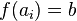 , para los
, para los  pertenecientes a
pertenecientes a
Proceso para resolver una ecuacion
El conjunto solución es aquel que contiene todos los valores determinados que cumplen con la ecuación, y estos valores son denominados soluciones. Por ejemplo, la ecuación
tiene a
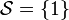 como su conjunto solución, con 1 como única solución de la ecuación.
como su conjunto solución, con 1 como única solución de la ecuación.En general, dada
 una función, y
una función, y 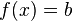 la ecuación que determina.
la ecuación que determina.El conjunto
 de valores de A es el conjunto solución si se cumple
de valores de A es el conjunto solución si se cumple 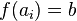 , para los
, para los  pertenecientes a
pertenecientes a
inecuaciones
Una inecuación es una desigualdad algebraica en la que sus dos miembros aparecen ligados por uno de estos signos:
| < | menor que | 2x − 1 < 7 |
| ≤ | menor o igual que | 2x − 1 ≤ 7 |
| > | mayor que | 2x − 1 > 7 |
| ≥ | mayor o igual que | 2x − 1 ≥ 7 |
Resolución de inecuaciones de primer grado
VALOR ABSOLUTO
Definicion de valor absoluto
La definición del concepto indica que el valor absoluto siempre es igual o mayor que 0 y nunca es negativo. Por lo dicho anteriormente, podemos agregar que el valor absoluto de los números opuestos es el mismo. 8 y -8, de este modo, comparten el mismo valor absoluto: |8|.También se puede entender al valor absoluto como la distancia que existe entre el número y 0. El número 563 y el número -563 están, en una recta numérica, a la misma distancia del 0. Ese, por lo tanto, es el valor absoluto de ambos: |563|.
La distancia que existe entre dos numeros reales, por otra parte, es el valor absoluto de su diferencia. Entre 8 y 5, por ejemplo, hay una distancia de 3. Esta diferencia tiene un valor absoluto de |3|.
Propiedades fundamentales
 |
No negatividad | ||||||||
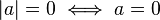 |
Definición positiva | ||||||||
 |
Propiedad multiplicativa | ||||||||
 |
Desigualdad triangular (Véase también Propiedad aditiva) |
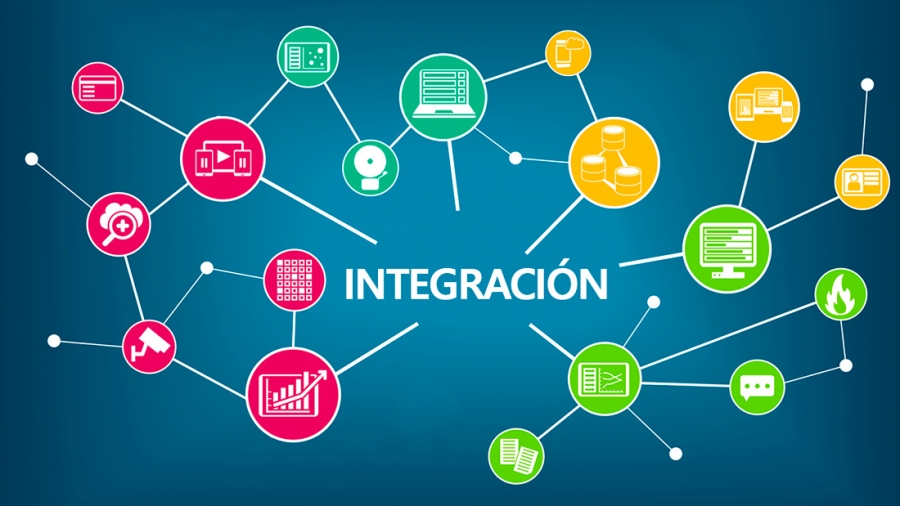
Usando la definición de valor absoluto se tiene:
Ecuaciones con valor absoluto de la forma │ax + b│= c


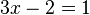
 .
. .
. 