Números complejos
Los números complejos conforman un grupo
de cifras resultantes de la suma entre un número real y uno de tipo imaginario. Un número real, de acuerdo
a la definición, es aquel que puede ser expresado por un número entero (4,
15, 2686) o decimal (1,25; 38,1236; 29854,152). En cambio, un número imaginario
es aquél cuyo cuadrado es negativo. El concepto de número imaginario fue
desarrollado por Leonhard
Euler en 1777, cuando
le otorgó a v-1 el nombre de i (de “imaginario”).
La noción de número
complejo aparece ante la imposibilidad de los números reales de abarcar a las
raíces de orden par del conjunto de los números negativos. Los números
complejos pueden, por lo tanto, reflejar a todas las raíces de los polinomios, algo que los números reales no
están en condiciones de hacer.
Gracias a esta
particularidad, los números complejos se emplean en diversos campos de las
matemáticas, en la física y en la ingeniería.
Por su capacidad para representar la corriente eléctrica y las ondas
electromagnéticas, por citar un caso, son utilizados con frecuencia en la electrónica y las telecomunicaciones. Y es que el
llamado análisis complejo, o sea la teoría de las funciones de este tipo, se
considera una de las facetas más ricas de las matemáticas.
Cabe resaltar que el
cuerpo de cada número real
está formado por pares ordenados (a, b).
El primer componente (a) es la
parte real, mientras que el segundo componente (b) es la parte imaginaria. Los números imaginarios puros son aquellos que sólo están formados por
la parte imaginaria (por lo tanto, a=0).
Los números complejos
componen el denominado cuerpo complejo (C).
Cuando el componente real a es identificado con el correspondiente complejo (a, 0), el cuerpo de estos números
reales (R) se transforma en un su
cuerpo de C. Por otra parte, C conforma un espacio vectorial de dos dimensiones sobre R. Esto demuestra que los números
complejos no admiten la posibilidad de mantener un orden, a diferencia de los
números reales.
Representación
Definición de números complejo
Definiremos cada complejo z como un par ordenado de números reales (a, b) ó (Re(z), Im(z)), en el que se definen las siguientes operaciones:
- Suma
- Producto por escalar
- Multiplicación
- Igualdad
A partir de estas operaciones podemos deducir otras como las siguientes:
- Resta
- División
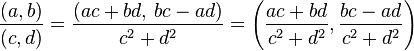
unidad imaginaria
- La unidad imaginaria es el número
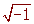 y se designa por la letra i.
y se designa por la letra i.

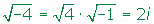
- Potencias

FORMA RECTANGULAR DE UN NUMERO COMPLEJO
-
Forma rectangular= z=a+bi
CONJUGADO DE UN NUMERO COMPLEJO

OPERACIONES DE NÚMEROS COMPLEJOS
-SUMA DE NÚMEROS COMPLEJOS
La suma de números complejos se realiza sumando partes reales entre sí y partes imaginarias entre sí.
(a+ bi) + (c + di) = (a + c) + (b + d)i
La suma tiene cuatro propiedades. Las propiedades son conmutativa, asociativa, distributiva y elemento neutro.
Propiedad conmutativa: Cuando se suman dos números, el resultado es el mismo independientemente del orden de los sumandos. Por ejemplo 4+2 = 2+4
Propiedad asociativa: Cuando se suman tres o más números, el resultado es el mismo independientemente del orden en que se suman los sumandos. Por ejemplo (2+3) + 4= 2 + (3+4)
Elemento neutro: La suma de cualquier número y cero es igual al número original. Por ejemplo 5 + 0 = 5.
Propiedad distributiva: La suma de dos números multiplicada por un tércer número es igual a la suma de cada sumando multiplicado por el tercer número. Por ejemplo 4 * (6+3) = 4*6 + 4*3
-RESTA DE NÚMEROS COMPLEJOS
La diferencia de números complejos se realiza restando partes reales e imaginarias entre sí (se resuelve de la misma forma que la suma)
( a + bi) − (c + di) = (a − c) + (b − d)i
-MULTIPLICACIÓN ENTRE NÚMEROS COMPLEJO
El producto de los números complejos se realiza aplicando la propiedad distributiva del producto respecto de la suma y teniendo en cuenta que i2 = −1.
(a + bi) · (c + di) = (ac − bd) + (ad + bc)i
-DIVISIÓN DE UN NÚMERO COMPLEJO


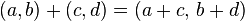


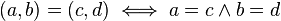

No hay comentarios:
Publicar un comentario