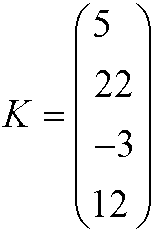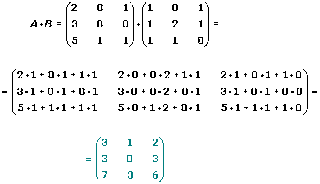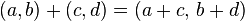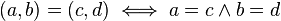RESEÑA HISTORICA
HISTORIA DE LAS MATRICES
Las matrices aparecen por primera vez hacia el año
1850, introducidas por J.J. SylvesterEl desarrollo inicial de la teoría
se debe al matemático W.R. Hamilton en 1853En 1858, A. Cayley introduce
la notación matricial como una forma abreviada de escribir un sistema de
m ecuaciones lineales con n incógnitas.
Las matrices se utilizan en el cálculo numérico, en la resolución de sistemas de ecuaciones lineales, de las ecuaciones diferenciales y de las derivadas parciales. Además de su utilidad para el estudio de sistemas de ecuaciones lineales, las matrices aparecen de forma natural en geometría, estadística, economía, informática, física, etc...
CLASES DE MATRICES
DEFINICIÓN DE MATRICES
Una matriz es un arreglo de números reales distribuidos en filas(donde una fila es cada una de las líneas horizontales de la matriz) y columnas,(es cada una de las líneas verticales de la matriz). cual están encerrados en paréntesis o corchetes. Las matrices generalmente se denotan con letras mayúsculas.
Ejemplos:
CLASIFICACIÓN Y PROPIEDADES DE LAS MATRICES
MATRIZ FILA:Una matriz fila está constituida por una sola fila pero varias columnas y su orden es 1xn
Ej A= 1X4 (2 3 5 2)
MATRIZ COLUMNA: Esta formada por una sola columna pero varias filas y su orden es nx1
Ej K=4X1
MATRIZ RECTANGULAR: tiene distinto número de filas que de columnas, siendo su dimensión mxn.

MATRIZ CUADRADA: tiene el mismo número de filas que de columnas es decir nxm m=n.
A= 3x3

CONCEPTOS ASOCIADOS
DIAGONAL PRINCIPAL: Los elementos de la forma a i j constituyen la diagonal principal donde i=j.
A=4x4

DIAGONAL SECUNDARIA:forman los elementos con i+j=n+1
A=4X4

LA TRAZA: Es la suma de los elementos de la diagonal principal y se denota.

MATRIZ TRIANGULAR SUPERIOR : Es una matriz cuadrada que tiene los elementos situados por debajo de la diagonal principal son iguales a ceros esto es a,i,j=0 si es mayor a J.
S=3x3

MATRIZ TRIANGULAR INFERIOR: Es una matriz cuadrada que tiene todos los elementos sobre la diagonal principal igual a 0 si i<1
H =4x4
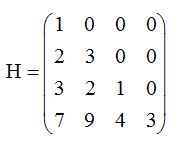
MATRIZ NULA: Es una matriz en las que todo los elementos son iguales a 0 y se lo representa
omxn
A=3X3
MATRIZ DIAGONAL: Es una matriz cuadrada que tiene todos sus elementos sobre y abajo de la diagonal principal= 0
a, i, j= i ≠ j

MATRIZ ESCALAR: Es una matriz cuadrada que tiene todos sus elementos sobre y bajo la diagonal principal igual a cero y los elementos de la diagonal principal son iguales entre si.
A=3x3
MATRIZ IDENTIDAD: Es una matriz cuadrada que tiene sus elementos iguales a cero excepto los de la diagonal principal que son iguales a uno y se denota Imxn.
OPERACIONES ENTRE MATRICES
SUMA ENTRE MATRICES
Dadas dos matrices de la misma dimensión, A=(aij) y B=(bij), se define la matriz suma como: A+B=(aij+bij).La matriz suma se obtienen sumando los elementos de las dos matrices que ocupan la misma misma posición.
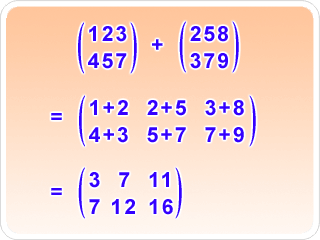
DIFERENCIA ENTRE MATRICES
Dadas dos matrices de la misma dimensión, A=(aij) y B=(bij), se define la matriz resta como A-B=(aij+bij).La matriz resta se obtienen restando los elementos de las dos matrices que ocupan la misma misma posición.

MULTIPLICACIÓN DE UNA MATRIZ POR UN ESCALAR
Dada una matriz A=(aij) y un número real k R,
se define el producto de un número real por una matriz: a la matriz del
mismo orden que A, en la que cada elemento está multiplicado por k.
R,
se define el producto de un número real por una matriz: a la matriz del
mismo orden que A, en la que cada elemento está multiplicado por k.
 R,
se define el producto de un número real por una matriz: a la matriz del
mismo orden que A, en la que cada elemento está multiplicado por k.
R,
se define el producto de un número real por una matriz: a la matriz del
mismo orden que A, en la que cada elemento está multiplicado por k.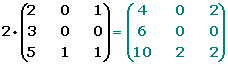
MULTIPLICACIÓN ENTRE MATRICES
Dos matrices A y B son multiplicables si el número de columnas de A coincide con el número de filas de B.
Mm x n x Mn x p = M m x p
El elemento cij de la matriz producto se obtiene multiplicando cada elemento de la fila i de la matriz A por cada elemento de la columna j de la matriz B y sumándolos.
POTENCIA ENTRE MATRICES

IGUALDAD ENTRE MATRICES
Dos matrices son iguales si
tienen las mismas dimensiones y cada elemento de la primera es igual al
elemento de la segunda que ocupa su misma posición. Es decir:
DETERMINANTES
MÉTODOS PARA ENCONTRAR LA DETERMINANTE DE UNA MATRIZ
El
determinante de una matriz suele utilizarse con frecuencia en
operaciones de cálculo, álgebra lineal y geometría descriptiva a un
nivel más complejo. Fuera del mundo académico, los ingenieros y los
programadores gráficos utilizas las matrices y sus determinantes
constantemente.[1] Si
sabes cómo hallar el determinante de una matriz de 2x2, las únicas
herramientas que tendrás que utilizar serán la suma, la resta y la
multiplicación.